La fuerza magnética 
que
actúa sobre una partícula cargada (con carga q
)
y que se mueve con velocidad 
en un campo magnético 
es:
La dirección de la fuerza magnética es perpendicular a ambos
vectores: a la velocidad y
al campo magnético .
La potencia suministrada a la partícula por la fuerza
magnética es 
Por lo tanto la fuerza no cambia la energía cinética de la partícula cargada,
sólo cambia la dirección de la velocidad de dicha partícula.
Si la velocidad tiene la misma dirección que el campo magnético,
no existe fuerza magnética sobre la partícula.
Para una partícula cargada moviéndose en un campo
magnético uniforme 
,
la velocidad puede ser representada como 
,
es la componente de la velocidad en
la dirección de B, cuyo valor no cambia.
La partícula avanza en la dirección de mientras
se mueve en círculo en un plano formado por 
y
.
La trayectoria resultante es una espiral con el eje en la dirección
de .
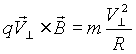,donde R es el radio de la espiral.
El momento de la partícula es: 
La velocidad angular del movimiento circular es: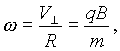 
¡La velocidad angular es independiente de la velocidad de la partícula cargada!
( 
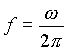es la frecuencia del ciclotrón).
La propiedad de mantenerse constante la frecuencia a pesar del aumento del radio de giro con cada vuelta permite construir un aparato llamado ciclotrón.
Este applet de java te pemite jugar con un ciclotrón.
El applet muestra una perspectiva desde arriba de una partícula moviéndose dentro del ciclotrón.
Pulsa aquí cyclotrón, para ver una foto de un ciclotrón real.
)window.location='http://www.edu.aytolacoruna.es/aula/fisica/applets/Hwang/ntnujava/cyclotron/cyclotron.jpg'){kind=link}
El cilindro formado por dos D- semiesféricas (abierto en la parte recta de la D) está hecho con hojas de cobre.
Las "des", se llaman así, forman parte de un oscilador eléctrico.
El oscilador establece una diferencia de potencial de signo alternativo entre las "des" (salto entre ellas).
Las "des" están inmersas en un campo magnético de dirección perpendicular a ellas (al plano de la pantalla) y sentido hacia adentro.
Supón que un protón parte del punto azul cerca del centro del ciclotrón, y que inicialmente se mueve hacía la "D" negativa.
La partícula es acelerada durante el tiempo que está entre las "des"...
Una vez dentro es apantallado ("protegido") del campo eléctrico por las paredes de cobre de la D.
El campo magnético no es apantallado por el cobre (nomagnético) de la D,
y por lo tanto el protón se mueve en una trayectoria circular.
En algún instante el protón emerge de la D para dar el salto entre las partes rectas y pasar de una D a la otra.
En el momento en que la partícula cruza, la diferencia de potencial también cambia de signo y
por lo tanto el protón acelera mientras encara nuevamente la D cargada negativamente.
Este proceso continúa y siempre que el protón está a punto de cruzar las "des", el potencial cambia de signo,
hasta que la espiral de giro del protón lo lleva al borde de la "D" y el protón sale disparado hacia fuera.
La frecuencia del oscilador eléctrico debe coincidir con la frecuencia de giro del protón (frecuencia del ciclotrón).
Si la distancia del salto entre las "des" es pequeña, las dos frecuencias son las mismas.
¿Qué pasa si el salto no es pequeño? Necesitarás ajustar la frecuencia del oscilador eléctrico.
Introduce el valor de la relación entre la frecuencia del oscilador y la del ciclotrón en el campo de texto.
(No olvides pulsar el botón ENTER después de cada cambio del valor de la relación).
Pulsa y arrastra arriba/abajo sobre el punto rojo que se encuentra dentro del símbolo del oscilador eléctrico para cambiar el voltaje del oscilador.
Pulsa Iniciar para comenzar la animación.
Un "click" del botón derecho del ratón para la animación y otro la reanuda.
La velocidad de la partícula cargada está representada por una línea amarilla.
La fuerza que actúa sobre la partícula está representada por una flecha roja.
Vy-Vx son las velocidades de la partícula cargada y se muestran a la derecha.
Pulsa Limpiar para borrar el rastro dejado por las trayectorias
Pulsa Reset para restaurar los valores por defecto.
La carga de un electrón es: 
y
su masa: 
,
Si la energía del electrón es 1eV (acelerado bajo el voltaje prefijado de 1V)
y el campo magnético es 1T (1 Tesla),
la frecuencia del ciclotrón será: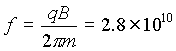 
(¡Es
muy grande!).
y la velocidad del electrón: 
(¡Se
mueve muy rápido!).
Si la velocidad es perpendicular al campo magnético, el radio del movimiento circular será :
(¡Es
muy pequeño!)
Si la velocidad sólo tiene un pequeño componente a lo largo del campo magnético (digamos el 1%),
el electrón se moverá en la
dirección del campo magnético con la velocidad: 
¡Imagina cómo se mueven los electrones bajo esas dos condiciones actuándo simultáneamente!
!Tus sugerencias serán muy estimadas! Please click hwang@phy03.phy.ntnu.edu.tw
Autor: Fu-Kwun Hwang, Dept. of physics, National
Taiwan Normal University
Traducción: José Villasuso Gato
Last modified : Otros applets en java de temas de Física